Welcome to the webpage of Information-Theoretic Machine Learning and Data Mining Laboratory. We are part of the Department of Mathematical Informatics at the University of Tokyo. We are interested in developing mathematical technologies for discovering latent knowledge in big heterogeneous and dynamic datasets and making quantitative predictions and detection.
Research Topics
- Fundamental Theory of Machine Learning and Data Science
- Information theoretic approach based on Minimum Description Length (MDL) principle and stochastic complexity
- Model selection/Dynamic model selection (Latent Dynamics)
- Latent variable modeling (Latent Structure Optimization)
- Network embedding with differential geometry
- Representation Learning
- Multi-view learning
- Ensemble learning
- Distributed cooperative learning
- On-line learning
- Basics of Data Mining
- Dynamic and heterogeneous data mining
- Anomaly detection
- Change detection/Change sign detection
- Network mining
- Stream mining
- Pattern mining
- Application of Data Mining
- Computer security/Malware detection
- Failure detection
- Market analysis/Advertisement impact analysis
- SNS analysis/Topic analysis
- Education data mining
- Traffic risk mining
- Medicine application (Glaucoma progression prediction)
Here are selected research topics:
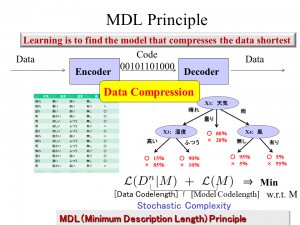
Learning with Minimum Description Length Principle
What is learning? We answer this basic question from the viewpoint of data compression. Suppose that a communication between an encoder and a decoder. The encoder tries to encode a raw data in a bit sequence and the decoder wants to decode it so that the original data is recovered. In this communication system, the encoder likes to encode the data sequence as shortly as possible for the sake of communication efficiency. How can we do realize this?
One way is to encode the data into two parts; model and exceptions. We have to encode both model and exceptions. If the model is too simple, the codelength for the model becomes short while that for exceptions becomes long. Meanwhile, if the model is too complex, the codelength for exceptions becomes short while that for the model becomes long. Thus by minimizing the total codelength for model plus exceptions leads to a reasonable model selection. Intuitively, this avoids overfitting data and oversimplification of models. This model selection principle is really based on the idea of data compression in the source coding scenario. We call the criterion for model selection induced from the data compression view the Minimum Description Length (MDL) Principle.
The MDL principle does not only match our intuition but also has solid theoretical backgrounds. Prof. Yamanishi's lifework is to clarify why the MDL works and how it can be universally applicable to a wide range of learning issues. See the book of Information-theoretic learning theory.
The tutorial on data science with the MDL principle will be given in KDD tutorial in 2019.
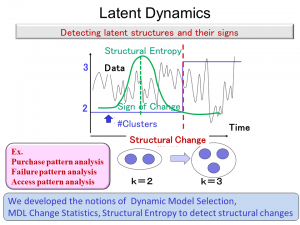
Latent Dynamics
We are concerned with the issue of how we can detect latent structure changes of probabilistic models from data streams. Here a latent structure means, e.g. the number of clusters in a clustering model, network structures, etc. We realize this task on the basis of the minimum description length (MDL) principle. That is, the change is determined so that the total codelength required for encoding the model sequence with its changes. We build a theory for detecting not only latent structure changes but also their signs. Specifically we have developed novel notions, which we call, Dynamic Model Selection(DMS), MDL change statistics, and Structural Entropy, for the purpose of latent structure change detection.
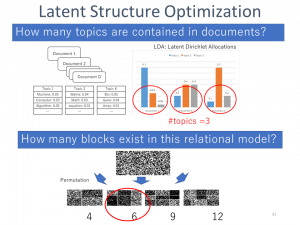
Latent Structure Optimization
We are concerned with the issue of estimating the optimal number of latent variable models. For example, estimating the optimal number of topics in Latent Dirichlet Allocation models, or estimating the optimal number of blocks in Stochastic Block models is extremely important. Note that in general, conventional information criteria cannot simply be applied to latent variable models since they are irregular in the sense that there is no one-to-one correspondence relation between parameters and probabilistic models. So we have developed a novel model selection criterion, which we call the Decomposed Normalized Maximum Likelihood Code-length Criterion(DNML) to resolve this problem. DNML works efficiently, are evaluated non-asymptotically, widely applicable to latent variable models, and have theoretical guarantees.
Medical Application: Glaucoma Progression Prediction
We work on massive heterogeneous cross-sectional and longitudinal datasets of visual field (VF), optical coherence tomography (OCT) and retinal measurements including retinal nerve fiber layer (RNFL), ganglion cell complex (GCC), and inner-plexiform layer (IPL) to predict, detect, and monitor glaucoma disease.
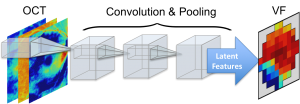
We have developed a number of cutting-edge machine learning techniques for predicting visual fields and for predicting and detecting glaucoma progression. Our team has recently focused on predicting visual fields from OCT measurements using deep learning.
We have multiple exciting projects in glaucoma and welcome highly motivated students to join our team.
Glaucoma: Glaucoma is an eye disease that damages the optic nerve and manifests both in structure (as in the optic nerve) and in function (as in the visual field) of the eye. Glaucoma gradually shrinks the peripheral vision.
Visual field (VF): VF test is used routinely to assess glaucoma which measures the sensitivity of the retina to tiny lights. Although VF analysis is a very well established area, VF testing is a time consuming task in clinics and this test frequently causes fatigue in patients and needs patient participation. VF tests are highly variable and non-stationary in nature which makes VF analysis a challenging task.
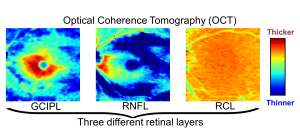
Optical coherence tomography (OCT): OCT is a pretty recent technology which captures cross-sectional pictures of the inner retinal layers. OCT examination is faster, less dependent on patients’ participation, and provides higher resolution and more robust measurements compared to VF test. Retinal nerve fiber layer (RNFL), ganglion cell complex (GCC), and inner-plexiform layer (IPL) can be extracted from OCT images using digital image segmentation software. Most of the commercial OCT instruments provide these measurements automatically.
VF prediction from OCT measurements: Figure below demonstrates how stacked convolution and pooling layers extract key latent features for OCT to VF transformation.